www.youtube.com/watch?v=aUNnGCxvAg0&list=PL_iWQOsE6TfVmKkQHucjPAoRtIJYt8a5A&index=4&t=1s

Part 1
Learning problems의 종류

1. Supervised Learning
- 가장 기본적인 알고리즘은 Classic linear regression problem
- 지도학습은 쉽게 말하자면, x라는 이미지가 주어졌을 때 라벨 y를 예측하는 문제
👉🏻 즉, 답(라벨)이 있고 이에 맞춰 함수(네트워크)를 훈련시키는 방식이다.
2. Unsupervised Learning
그렇다면 unlabeled data는 어떻게 다뤄야 할까?
(사실 대부분의 데이터는 라벨을 가지고 있지 않기 때문에)
👉🏻 네트워크를 통해 representation를 뽑아내어 그 안에서의 특징들을 찾는 방식이다.
3. Reinforcement Learning
👉🏻Agent가 action을 취하여 Enviroment를 형성하고 이 environment가 다시 agent에 영향을 미치는 방식이다.
먼저, Supervised Learning에 대해 알아보자.

- 데이터와 이에 대한 answer(label)이 주어졌을 때, 이 쌍을 가지고 네트워크 파라미터를 훈련시킨다.
이런 네트워크는 고차원의 polynomial(다항식)과 같은 형식이 될 수도 있고 그냥 일차식의 형태도 될 수도 있다.
- 그럼 이런 훈련된 네트워크를 통과시켜 나온 값 $ f_\theta (x_i) $와 $y_i$간의 차이를 어떤 식으로 쓸 수 있을까?
뭐 흔하게 쓰는 차를 제곱하는 방식이나 dirac delta와 같이 답이면 1, 아니면 0과 같은 loss function을 사용할 수 있을 것이다.
- 이렇게 계산한 difference (loss function)을 최적화하기 위해 어떤 방식을 사용할 수 있을까?
대표적으로는, 적절하게 gradient를 빼서 최소값으로 가는 gradient descent방법을 사용할 수도 있다. 이에 대한 내용은 뒤에서 자세하게 다룬다.
다음은 Unsupervised Learning이다.

Unsupervised Learning은 단어에서도 알 수 있듯이 답이 없는 방식(비지도)으로 학습된다.
세상에 많은 데이터는 아마 label이 주어지지 않은채 존재한다. 사실 label과 쌍으로 존재하는 경우는 인위적인 경우가 대부분일 것이다. 이런 unlabeled data로부터 특징을 찾아내어 "잘" representation하는 것이 unsupervised learning의 목적이라 할 수 있다.
- 대표적인 unsupervised learning인 Generative modeling에 대해 생각해보자. 이미지를 만들어내는 GAN과 같은 네트워크를 생각할 수 있다. 이외에도 VAE, pixel RNN등이 있다.
- 다음으로는 self-supervised representation learning이 있는데 많이들 아는 언어모델인 BERT와 GPT모델이 있다. 이는 문장을 인풋으로받아 meaningful representation을 만들어내고 downstream task(ex. 문장분류)에서 이를 이용하여 문제를 해결하는 방식이다.
세번째는 Reinforcement Learning이다.

강화학습은 좀 더 복잡한 형태를 가진다. 이미지와 같은 인풋을 라벨에 매칭시키는 형태가 아닌 "Behavior(행동)"에 대한 학습방식이다.
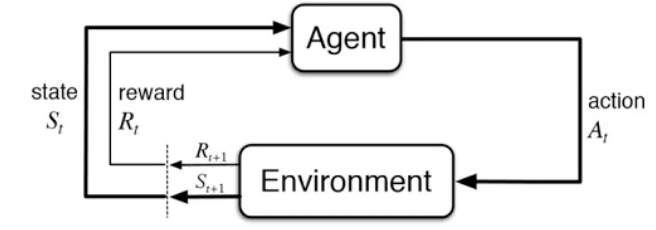
- Agent가 임의의 프로세스에서 액션을 취하고 그 결과인 환경에 영향을 받고 그런식으로 훈련이 된다.
- 당시 최선인 액션이 아닌 길게 봤을 때 best 결과를 뽑아내도록 액션을 취하게 된다.
- 체스게임으로 예를 들어 설명하자면 체스 게임 중 한 수를 둘 때는 최종 승리를 위해 길게 보고 액션을 취하지 당시에 최선이 되는 수를 두지 않는다. 이와 같이 강화학습은 일종의 supervised learning의 일반화 버전이라 생각할 수 있다.
(라벨은 최종승리)
- 하지만 강화학습은 supervised learning보다 어려운데 라벨이 직관적이지 않고 명확하지 않기 때문이다.
- 예를 들자면, 강화학습은 강아지를 훈련시킬 때 여러 액션을 통해 간식을 받게 되는 경우로 설명할 수 있다.
또, 이커머스 회사를 예로 들자면, 판매하고 구입하고 여러관찰을 통해 최종 reward인 이익을 얻는 순환 circle을 강화학습에 비교할 수 있다.
Part 2

Supervised Learning에 대해 더 깊게 알아보자.
많은 실생활에서 쓰이고 있는 Learning이다.
앞에서도 설명했듯이, 어떤 input과 label쌍이 주어졌을 때 이 관계를 잘 표현하도록 네트워크를 훈련시키는 방식이다.
대표적인 예로는,
1. Image를 기반으로 Category를 예측하는 경우
2. 영어 문장을 기반으로 프랑스어 문장 예측(번역)
3. X-ray 이미지를 기반으로 병의 유무 예측
4. 음성을 기반으로 텍스트를 예측(speech to text)
💢 하지만 많은 경우에서 예측이란 쉽지 않다.
예를 들어 다음과 같은 이미지들이 주어졌을 때 어떤 숫자인지, 문자인지 어떻게 구분할 수 있을까?

다음과 같이 각 숫자에 대한 확률값을 생각해볼 수 있다.

그럼 어떻게 예측을 할 수 있을까?
Training set이 주어졌을 때 $f_\theta (x) $를 학습을 조건부 확률 관점에서 생각해보자.

x를 Input을 represent하는 랜덤 변수, y를 output을 represent하는 랜덤 변수라 생각해보자.
위의 조건부확률은 chain rule과 정의에 의해 이렇게 쓰일 수 있다.

그럼 어떻게 $p(y|x)$를 표현할 수 있을까?

Input이 주어졌을 때 computer program에 통과시켜 확률값을 얻을 수 있다.
그럼 이 computer program은 무엇을 뜻할까?
앞의 예시로 돌아가보자.

왼쪽과 같이 이미지가 주어졌을 때 각 label에 대한 확률값을 얻을 수 있다.
이러한 확률값을 얻기위해 computer program에 대한 식을 파라미터(theta)를 이용하여 다음과 같이 쓸 수 있다.

(input x가 주어졌을 때 dog일 때의 확률과 cat일 때의 확률)
이런 조건부확률을 함수로 표현해보면 다음과 같다.

각 class에 대해 얻은 값을 softmax라는 함수를 취해 0과 1사이의 최종 조건부 확률을 얻게 되는데 여기서 softmax가 아닌 다른 함수도 사용가능하다.(one-to-one & onto, 즉 일대일 대응 함수이면 이상적이다.)
(사실, 머신러닝에서 위와 같은 함수를 선택할 때 딱 정답이 있는 것은 아니다. 사실 데이터를 잘 represent하면 된다. data에 대한 정보를 잃지만 않으면 된다.)
그럼 어떻게 softmax와 같은 함수를 사용하게 되었을까?
1. 위의 $f_{dog}(x)$와 같은 함수값은 positive(양수)가 되어야한다. 확률값은 항상 0보다 크거나 같기 때문이다.
어떤 수를 양수로 만드는 데에는 다음과 같은 방법이 있다.

제곱하거나, 절대값을 취하거나, 음수보다 작다면 0을 택하거나 등등 여러 방법이 있다.
하지만 앞의 세 방식은 일대일 대응이 아니다.(한 y값에 대응하는 여러개의 x값이 존재할 수 있으므로)
따라서 exponential형태인 네번째 경우를 사용하는 것이 편리하다.
2. 또한, 확률값은 0과 1사이의 값이 되어야 한다.
값들을 0과 1사이로 만드는데에는 다음과 같은 방법이 있다.(normalization이라 볼 수 있다.)

이외에도 min값을 빼고 max값으로 나누어 0과 1사이로 만들 수 있다.
정리해보면 softmax는 다음과 같다.

시각화해보면 다음과 같다.
<1D case>

<2D case>

🌟
이제 softmax의 형태가 왜 나왔는지에 대해 알게 되었다.
그럼 "softmax"라는 이름은 왜 나온것일까?
다음은 exponential부분에 곱해진 파라미터에 따른 함수 그래프이다.
파라미터가 커질 수록(100인 경우) 마치 계단형태인 step function($max \theta_y x$)과 비슷해지고, 적을수록(1인 경우) soft해진다.
softmax는 이 파라미터가 1인 경우이므로 매우 soft한 max함수이므로 softmax라 불려지게 되었다.

Part 3 : Loss function
머신러닝 프로세스는 다음과 같이 정의될 수 있다.
1. Define model class
2. Define loss function
3. Pick your optimizer
4. Run on GPU
그럼 이 네트워크의 파라미터를 어떻게 정할까?
그전에 더 기본적인 질문에 대해 생각해보자.
어떻게 데이터셋이 만들어질까?
데이터셋에 대한 핵심 가정은 Independent and indentically distributed(i.i.d.) 이다.
(데이터끼리 서로 독립이고 동일하게 분포되어있다는 가정)

앞서 말했듯이 우리는 true $p(y|x)$를 알아맞춰야 한다. 즉 input x에 대한 label y를 정확하게 알아내는 것이 핵심이다.
이를 위해 적절한 parameter $\theta를 선택해야 한다.

위의 식 $p(\mathcal{D})=\prod_{i} p\left(x_{i}\right) p_{\theta}\left(y_{i} \mid x_{i}\right)$ 에서
$p(x_i)$는 0과 1사이의 확률값이다.
양변에 로그를 취해보면,
$\begin{equation}
\log p(\mathcal{D})=\sum_{i} \log p\left(x_{i}\right)+\log p_{\theta}\left(y_{i} \mid x_{i}\right)=\sum_{i} \log p_{\theta}\left(y_{i} \mid x_{i}\right)+\text { const } \end{equation}$
와 같이 된다. 이를 maximize/minimize하기 위해 parameter를 선택하여 학습을 하게 된다.

학습을 위해 정의하는 loss function은 보통 얼마나 parameter $\theta가 "나쁜"지에 대해 양을 측정한다.
예를 들어, 다음과 같은 loss function들이 있다.
1. negative log-likelihood
$-\sum_{i} \log p_{\theta}\left(y_{i} \mid x_{i}\right)$이 있다.
(a.k.a cross-entropy)

2. zero-one loss
$-\sum_{i} \delta\left(f_{\theta}\left(x_{i}\right)=y_{i}\right) $
쉽게 말하자면 답이면 1, 아니면 0을 주는 dirac delta function이다.
3. Mean squared error
$\begin{equation}
\sum_{i} \frac{1}{2}\left\|f_{\theta}\left(x_{i}\right)-y_{i}\right\|^{2}
\end{equation}$
말그대로 에러를 제곱하여 평균낸 값이다.
Part 4 : Optimization

모델도 선택했고 loss function도 선택했다. 이제 어떻게 파라미터를 훈련시켜야 할까?
이에 대한 내용이 optimization이다.
이는 theta를 어떻게 "move"시킬 지에 대한 내용이다.(어떤 방향으로 이동시킬 것인가?)
1. Gradient descent

간단하게 1D에서 생각해보자.

점이 다음과 같이 있을 때 함수값을 minimize하기 위해서는 gradient의 부호와 반대로 x값을 움직여야한다.

종합해보면 Gradient descent는 다음과 같다.

기본적인 모델인 Logistic regression에 대해 알아보자.
Logistic regression

이 중, Class가 2개만 있을 때를 고려해보자.(binary classfication)

위에서 배운 softmax는 다음의 과정을 거쳐 sigmoid 함수가 된다.
Empirical risk minimization
Empirical risk는 한글로 뭐라 번역해야 적절한지 모르겠지만 경험적인 리스크다. 즉, 모델은 경험(training data)으로부터 배우는데 이에 대한 risk이다.
이에 반해, True risk는 실제 데이터에 적용했을 때에 대한 risk이다. 즉, 학습에 사용되지 않은 데이터를 적용시켰을 때에 대한 risk이다. 이 risk가 모두 낮은 경우가 이상적인 경우이다. 이상적이지 않은 경우를 두 가지로 나눈다면 다음과 같다.
Overfitting : Empirical risk는 낮지만 true risk는 높은 경우이다.
원인
- 데이터셋이 너무 적을 때
- 모델이 너무 강력할 때(너무 파라미터가 많을 때)
Underfitting : Empirical risk와 true risk가 모두 높은 경우이다.
원인
- 모델이 너무 약할 때(파라미터가 적음)
- optimizer가 잘 설정되지 않은 경우(ex. wrong learning rate)
(Empirical risk는 높은데 true risk가 낮은 경우는 오류이다...)
Lecture 2를 요약하자면 다음과 같다.

'개발 > UC Berkely CS182' 카테고리의 다른 글
| [Lecture 5] Backpropagation (6) | 2021.04.18 |
|---|---|
| [Lecture 4] Optimization (2) | 2021.04.11 |
| [Lecture 3] Error Analysis (2) | 2021.04.04 |
| [Lecture 1] Introduction (2) | 2021.03.20 |
| [시작] Deep Learning: CS 182 Spring 2021 (0) | 2021.03.20 |





댓글