https://www.youtube.com/watch?v=VKPkM6jt_P0
Part 1 : Generating Images from CNNs
전까지 네트워크의 작동원리, 배치, 정규화와 같은 방법론에 대해 배웠다.
그럼 CNN와 같은 convolutional network같은 경우에 층을 거치면서 어떠한 데이터, 이미지를 "보는" 것일까?
이를 시각화해보고 확인해보고 싶은 생각이 자연스럽게 들 것이다.
이러한 확인을 통해 네트워크를 이해하고 좀 더 발전시킬 수 있기 때문이다.

이번 파트에서는 이러한 시각화에 대해 배운다.
어떤 것을 시각화해볼 수 있을까?/ 시각해보고 싶을까?
<1 >첫번째로는 filter 그 자체이다. weight라고도 말할 수 있다.
어떤 이미지 feature가 필터를 통해 나오는 것일까? 어떤 이미지의 부분이 나오는 것일까?
예를 들어, 강아지를 인식한다고 할 때 특정 필터를 시각화해본다면 이 필터를 통해 귀와 같은 feature가 나오는 지 확인해볼 수 있기 때문이다.

<2> 두번째는 뉴런을 활성화시키는 Stimulti다.
예를 들어 어떠한 이미지 패치가 output 값을 크게 만드는 지(활성화 시키는지)를 시각화해보는 방법이다.
이를 통해 이미지 내의 어떤 부분이 특정 물체를 인식하는데에 중요한 지 확인할 수 있다.
🌟 그럼 이를 어떻게 확인해볼 수 있을까?
1) 첫번째 방법으로는 이미지 내에서 쭉 슬라이딩 윈도우를 하며 output이 큰 패치를 찾아내는 방법을 사용할 수 있다.

위와 같은 강아지 사진 경우에 저 빨간박스 패치가 가장 높은 값을 보여주는데 이는 저 filter가 눈과 같은 특징을 활성화한다고 해석할 수 있다.

2) 두번째 방법으로는 어떤 이미지 픽셀이 값에 영향을 가장 크게 미치는 지를 확인하는 방법이 있다.
여기서 "영향을 미치는"이 의미하는 바가 무엇일까?
특정 픽셀이 특정 유닛을 어느정도 바꾸는 지 측정하면 된다. 여기서 나오는 것이 "gradient"이다.
Gradient값 자체가 특정 값에 대해 얼마나 변하는 지를 가르키는 값이기 때문이다.
그럼 이 gradient를 어떻게 계산하면 될까? 앞에서 배웠던 back propagation 방법을 사용하면 된다.

그럼 실제로 gradient로 시각화한 이미지를 확인해보자.
아래 왼쪽 그림은 gradient이고 오른쪽은 약간의 수정된 버전이다. "Guided backpropagation"인데 나도 여기서 처음 봐서 신기했다. 눈으로 봐도 더 선명하게 gradient를 체크할 수 있기 때문이다.
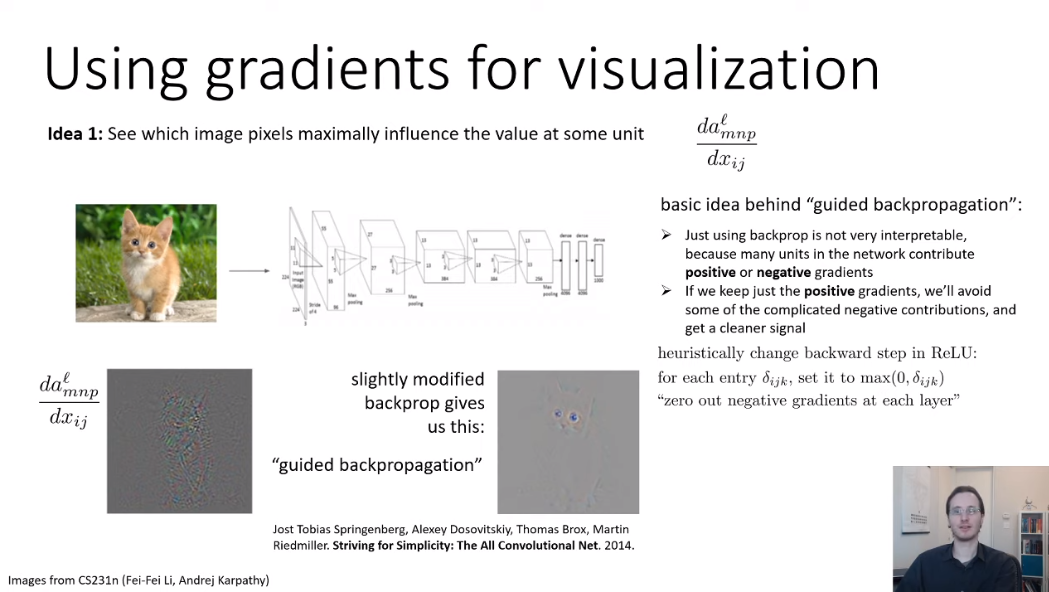
사실 gradient를 계산하면 음수값도 나오기 때문에 복잡해지는데, guided backpropagation은 gradient에 ReLU를 취해서 좀 더 단순화한 방법이다. 즉, 음수 gradient를 0으로 없애버리는 방법이다.

직관적으로는 정보를 너무 없애는 게 아닌가 싶지만 실제 사용해서 위에서도 확인했듯이 좀 더 깔끔한 시각화 이미지를 볼 수 있어 흔히 사용한다.

티스토리에 이모티콘이 생겼네요.. 귀엽다..(뜬금)
Part 2 : Visualizing Features with Backpropagation
두번째 파트에서는 Back propagation으로 어떻게 feature를 시각화하는지에 대해 좀 더 자세하게 다룬다.
앞파트에서는 gradient를 이용하여 어떤 이미지 픽셀이 유닛 값에 영향을 가장 많이 끼치는 지를 보았다.
두번째로 gradient를 사용하여 시각화하는 방법으로는 이미지를 "최적화"하여 최대로 특정 유닛을 활성화시키는 방법이 있다.

예를 들어 고양이 이미지에서 gradient를 시각화했을 때 눈 부분이 파랗게 나왔다고 해보자. 그럼 이를 더 활성화 시키기 위해서 blue channel을 1,000,000,000으로 만들면 어떻게 될까? 그야말로 "미친"이미지가 된다. 이를 위해 제어해주는 regularization term을 뒤에 추가해주어야 한다.

여기서 중요한 디테일은 softmax 적용전에 maximizing시켜야 한다는 것이다.

시각화하는 방법은 다음의 단계를 따른다.
1. gradient를 이용하여 이미지를 업데이트 시킨다.
2. 약간 블러처리한다.
3. 작은 값은 0으로 처리한다.
4. 1-3단계를 반복한다.
이를 시각화한 이미지는 다음과 같다.

다음은 7번째 레이어와 8번째 레이어에서의 시각화이미지를 보여주는데 레이어가 뒤로 갈수록 좀 더 rough한 feature를 보여주는 것을 볼 수 있다. 앞쪽 레이어일수록 finer detail, 즉 세밀한 디테일을 시각화한다.


Part 3 : Deep Dream & Style Transfer
Lecture 9의 마지막 파트에서는 위에서 배운 시각화 지식을 가지고 이미지를 어떻게 "수정"하는지에 대해 배운다. 각 층에서 어떤 정보들을 가지고 있는지 시각화를 통해 배웠다면 어떤 층에서 조금 "수정"을 해서 스타일을 바꿀 수 있는지를 알 수 있기 때문이다. 이를 "Style Transfer"라고 한다.

Style Transfer에 들어가기 전에 DeepDream에 대해 알아보자.
이건 나도 처음 들은 용어인데, 예를 들어 구름에서 패턴을 찾는다고 해보자.
누구나 강아지나 고양이 또는 다른 물체처럼 생긴 구름을 본 경험이 있을 것이다.
DeepDream은 이러한 아이디어를 이용하는데, 한 레이어를 고르고 좀 더 활성화시켜 아래의 그림처럼 특정 물체처럼 보이게 만든다.


그럼 하나의 이미지에서 특징들을 과장시키는 것 대신에 하나의 이미지가 다른 이미지처럼 보이게 만드는 건 어떨까? 예를 들어 피카소의 화풍으로 풍경화를 바꾸는 등의 작업을 생각할 수 있다.
즉, Content를 유지하고 Style만 바꾸는 작업이라 할 수 있다.
🌟 그럼 Style은 어떻게 정량화시킬 수 있을까?

앞에서 우리는 각 레이어에서의 output을 시각화하는 방법에 대해 배웠는데 이를 여기에 적용시킬 수 있다.
이를 이용하면 이미지에서 어디에 curve가 있는지 직선이 있는지에 대한 정보를 알아낼 수 있다.
여기서 하나의 질문이 있을 수 있다.
Q. 어떤 특징들이 함께 나타날까?
이 질문에서 자연스럽게 통계의 Covariance를 생각해볼 수 있다.
또, 이 공분산을 통해 Gram Matrix이 나오게 된다.

이 Gram matrix를 통해 새로운 이미지를 생성해낼 수 있다.
(Loss function을 source image와 new image의 Gram matrix의 차로 정의하여 최적화시키는 방식)

🌟 그럼 Content는 어떻게 정량화시킬 수 있을까?
위에서 보았듯이 각 레이어를 통과시키면 이미지의 feature가 나오게 된다.
이 아이디어를 이용하여 몇개의 layer를 통과시킨 feature간의 차이를 줄이는 식으로 Loss function을 정의하면 content 또한 유사하게 new image를 만들어낼 수 있다.

따라서 Style transfer를 종합하면 다음과 같다.
앞서 설명한대로 Content Loss는 왼쪽과 같이 정의되고 Style Loss는 오른쪽과 같이 정의된다.

'개발 > UC Berkely CS182' 카테고리의 다른 글
| [Lecture 12] Transformers (0) | 2021.06.07 |
|---|---|
| [Lecture 10] Recurrent Neural Networks (0) | 2021.05.23 |
| [Lecture 8] Computer Vision (2) | 2021.05.09 |
| [Lecture 7] Initialization, Batch Normalization (0) | 2021.05.02 |
| [Lecture 5] Backpropagation (6) | 2021.04.18 |





댓글