모델 기반
앞선 포스팅에서는 메모리 기반의 collaborative filtering에 대해 다뤘다.
https://simonezz.tistory.com/22
추천시스템 Collaborative Filtering(CF) 정리 (Python 기반) - 1
Collaborative Filtering이란 무엇인가? 위의 그림에서도 알 수 있듯이 특정 사용자 A에게 컨텐츠(영화, 뉴스기사 등)를 추천하고자 할 때 취향이 비슷한 사용자의 취향에 기반해 추천을 하는 것이다. 즉 이제까..
simonezz.tistory.com
이제 모델 기반의 방법들에 대해 알아보자.
여기서는 sparse한 user-item matrix를 압축하거나 줄이는 방법 또한 포함하고 있다.
이를 위해서 Dimensionality Reduction에 대해 잠시 다뤄보자.

Dimensionality Reduction
User-item matrix에는 두 개의 차원이 있다. (사용자들의 수, 아이템들의 수)
행렬이 대부분 비어있다면 차원을 축소함으로써 시간상으로나 공간상으로나 효율적으로 만들 수 있다.
이를 위해서는 Matrix factorization이나 autoencoders가 사용될 수 있다.
Matrix Factorization
Matrix Factorization(행렬 분해?)는 큰 행렬을 작은 행렬들로 쪼개는 과정이라 볼 수 있다.
사실 대학원 첫학기 때 자세히 배워서 익숙한데 보통 추천시스템에서는 어떤 방법을 사용하나 보자.

위 그림에서 보면 한 mXn matrix가 mX2, 2Xn의 두 개의 행렬(latent factor라고 한다)로 분해되는 것을 알 수 있다.
또 원래 matrix에서의 4라는 값은 2*2.5 + -1*1 로 분해된 것을 볼 수 있다.

이렇게 두개의 latent factor로 분해함으로써 사용자와 아이템의 숨겨진 특성들을 알 수 있다.
여기 factorization에 대한 가능한 해석들이 있다.
- 사용자 vector (u,v)에서 u는 얼마나 이 사용자가 호러 장르를 좋아하는 지, v는 얼마나 이 사용자가 로맨스 장르를 좋아하는 지에 대한 지표이다. 즉 각 column은 장르를 뜻한다.
- 따라서 위의 사용자 vector (2, -1)를 통해 이 사용자는 호러를 좋아하고 로맨스 장르를 안좋아한다고 할 수 있다.
- 아이템 vector (i, j)에서 i는 얼마나 이 영화가 호러장르인지, j는 얼마나 이 영화가 로맨스장르인지에 대한 지표이다.
- 따라서 위의 아이템 vector (2.5, 1)은 이 영화가 2.5정도의 호러성과 1정도의 로맨스성을 가지고 있는 것을 알 수 있다.
- 그래서 이 영화는 호러장르에 속하고 사용자는 이 영화에 5점을 줄 수도 있었지만 약간의 로맨스 성질로 인해 4점으로 평가 점수가 깎였다고 말할 수 있다.
이렇게 factor 행렬들은 사용자와 아이템에 대한 통찰을 준다.
하지만 현실에서는 당연히 더 복잡하다. 이러한 factor가 100개 1000개까지 될 수 있다.
그래서 모델을 training하는 과정에서 최적화가 필요하다.
Latent factor의 수는 추천에서 많은 영향을 미친다. Factor의 수가 많아질수록 추천이 더 개인에게 맞춰지기 때문이다.
하지만 너무 많은 factor는 overfitting으로 갈 확률이 높다.
Matrix Factorization 알고리즘들
아마 Matrix Factorization에서 가장 유명한 알고리즘은 당연 Singular Value Decomposition이다.
이외에도 PCA, NMF등이 있다. Autoencoders 또한 dimensionality reduction에 사용된다.
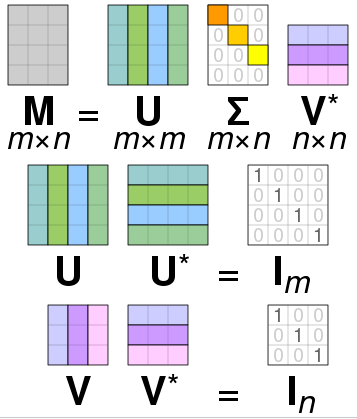
파이썬을 이용하여 추천시스템을 만들어보자.
여기서는 scikit의 surprise를 이용하여 구현했다.
먼저 저번 포스팅에서 다뤘던 메모리 기반의 추천시스템부터 만들어보자.
메모리 기반 CF 구현
추천 함수에 사용할 알고리즘을 선택하는 건 어떤 기술에 적용하냐에 따라 다르다.
여기서는 Centered k-NN(k-Nearest Neighborus)를 사용해 구현해 보았다.
surprise에서 KNNWithMeans를 사용할 수 있다.

유사도 측정을 위해 딕셔너리를 추천 함수 즉 kNN함수에 넣어줘야 한다. 이 딕셔너리는 required keys를 갖고 있어야 하는데 예를 들면, name, user_based, min_support가 있다.
- name은 사용할 유사도 metric을 가지고 있다. 이 metric으로는 cosine, msd, pearson 또는 pearson_baseline 이 있다. 디폴트는 msd이다.
- user_based는 boolean으로 이 방법이 user-based인지 item-based인지에 대해 말해준다. 디폴트는 True로 user-based 방법을 사용할 거라는 뜻이다.
- min_support는 유사성을 고려하기 위한 사용자들 사이의 필요한 최소 공통 아이템 수이다. item-based 방법 경우에는 두 아이템의 공통사용자의 최소 수를 뜻한다.

surprise로부터 KNNWithMeans함수를 import한다.
또 위에서 말한 함수 옵션을 similarity metric은 cosine으로 user_based는 False로 설정해 item-based 방법을 사용한다.

사용자 E의 영화 2에 대한 평점을 4.15로 예측하는 것을 볼 수 있다.

메모리 기반 CF 말고 모델 기반 CF도 한 번 실행해보자.
https://surprise.readthedocs.io/en/stable/matrix_factorization.html
Matrix Factorization-based algorithms — Surprise 1 documentation
Parameters: n_factors – The number of factors. Default is 20. n_epochs – The number of iteration of the SGD procedure. Default is 20. init_mean – The mean of the normal distribution for factor vectors initialization. Default is 0. init_std_dev – Th
surprise.readthedocs.io
위의 사이트에서 자세한 파라미터 사항을 알 수 있다.

surprise 라이브러리 안의 movielens dataset을 다시 한번 사용한다.

movielens dataset을 data로 불러오고 그 안의 raw_ratings중 user, item, rate, id를 불러온다.
만약 여기서 id 열을 지우고 싶다면 del df['id']로 지울 수 있다.
이 데이터로 피봇 테이블을 만들어보자. 피봇 테이블이란 자기가 원하는 데이터를 재배치한 테이블이라 생각하면 된다.
피봇 테이블에 대해 쉽게 설명한 글 : https://m.blog.naver.com/PostView.nhn?blogId=zxcvbnm6386&logNo=221222494922&proxyReferer=https:%2F%2Fwww.google.com%2F

x축이 상품이고 y축이 사용자 아이디인 평점 행렬 df_table를 만든다. 즉, 각 행은 사용자의 영화들에 대한 평점이고 각 열은 한 영화에 대한 사용자들의 평점이다.
set_index는 dataframe을 인풋으로 하여 기존의 컬럼들을 이용해 새로운 dataframe을 만들어준다.

.unstack() 은 행 인덱스를 열 인덱스로 변환시켜준다.

다음은 unstack()을 안해줬을 때이다.
위의 table의 user와 item을 인덱스로 설정하였음을 확인할 수 있다.

unstack()을 해줬을 때는
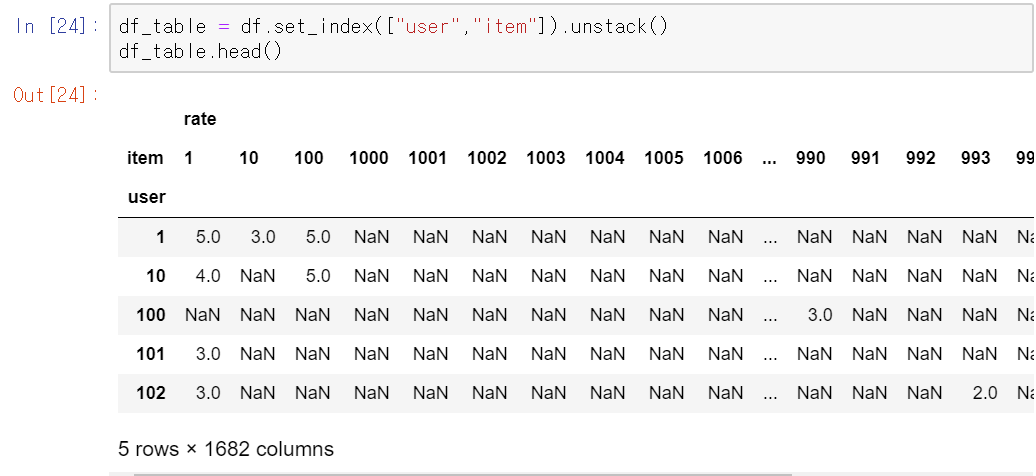
행인덱스를 열인덱스로 변환했을 때 왜 이렇게 나오는지 이해가 안가서 더 찾아보았다.
그리고 왜 이름이 unstack인지 궁금해서 찾아보았다.
stack은 말그대로 쌓다는 건데 unstack는 쌓다의 반대인 옆으로 늘어놓는 것일 테다.

이 그림을 보니 이해가 간다.
위에 user, item을 인덱스로 설정하여 왼쪽 그림과 같이 쌓아진 형태였다면
unstack을 통해 user는 행 인덱스, item는 열 인덱스가 되는 것이다.
이제야 왜 이름이 이런지 결과가 이런지 이해가 간다.
다시 돌아와, 만든 테이블을 보면 대부분의 값이 NaN으로 채워져 있다.
어찌보면 당연한 일이다. 사용자들이 본 영화가 일부분이니 말이다.
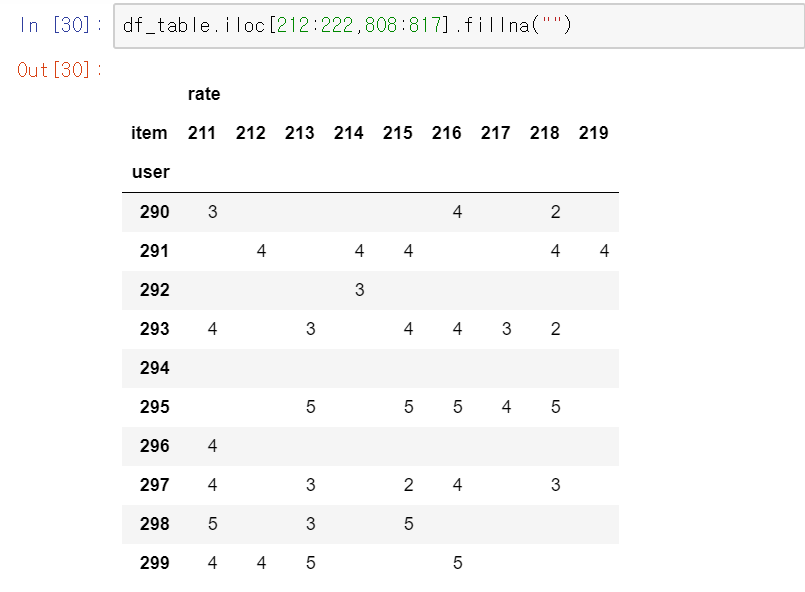
얼마나 sparse한지 쉽게 보기위해
iloc를 이용하여 특정 인덱스 범위의 table을 가져오고 fillna(N/A나 NaN을 특정값으로 채움)를 이용해 NaN값을 ""로 채웠다.
plt을 이용해 시각적으로 봐보자.

평점이 점으로 나타난다.
리마인드를 위해,

SVD를 이용해 예측을 해보자.
위에서 보았듯이 평점 행렬은 sparse행렬이므로 SVD를 바로 적용하기 힘들다. 따라서 오차함수에 대해 최소화하는 방법을 사용한다.

Surprise의 minimization알고리즘은 Stochastic Gradient Descent방법을 사용한다.
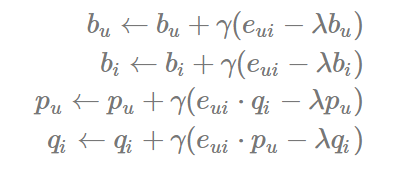
또 Surprise의 SVD의 주요 파라미터로는 n_factors, n_epochs, lr_all 이 있다.

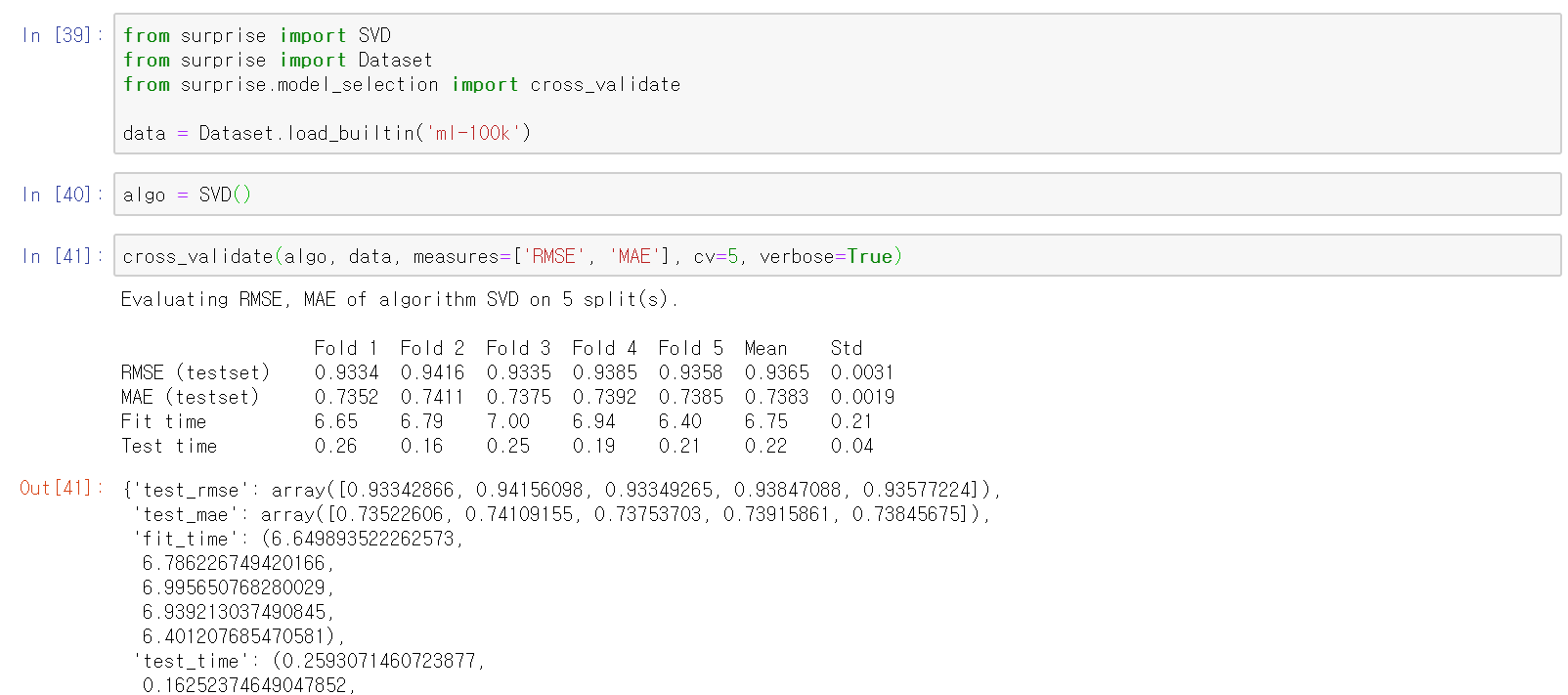
cross validation을 이용해 간단하게 실행해볼 수 있다.
하지만 전체적인 과정에서 확인해보고 싶기 때문에 surprise말고 다른 걸 써보려고 한다.
SVD를 이용하여 CF를 구현해보자.
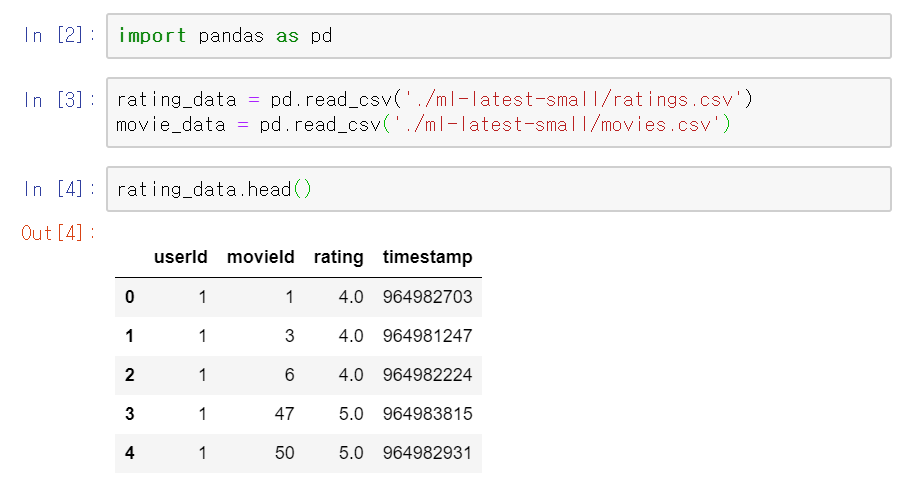
마찬가지로 movielens dataset을 사용한다.
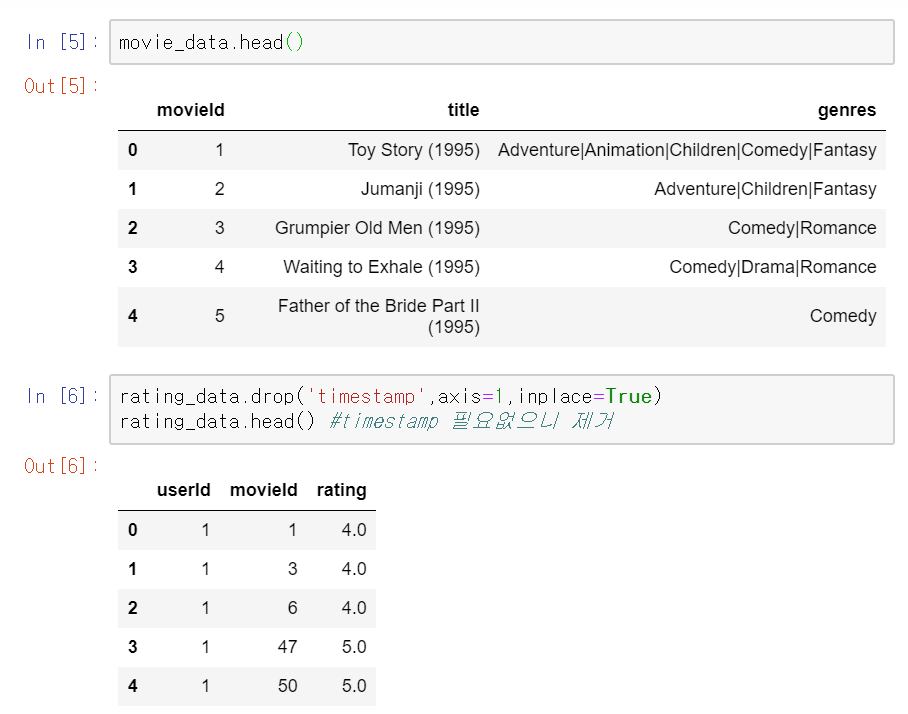
필요없는 timestamp 열을 제거한다.

마찬가지로 영화데이터에서도 장르를 제거한다.

rating_data와 movie_data의 공통 열인 movieId를 이용해 merge하여 합친다.
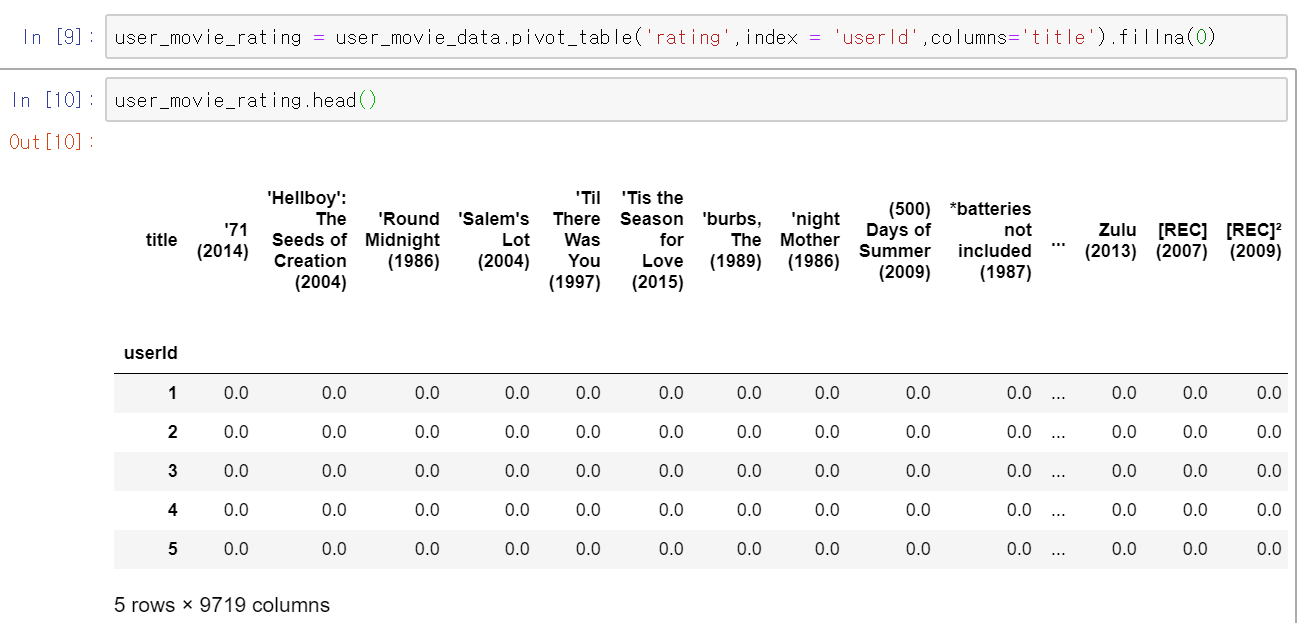
위에서도 사용했던 pivot table을 이용해 index는 userId로 하고 행렬값은 평점, 그리고 column은 각 영화 제목으로 하여테이블을 만든다. 평가되지 않은 항목에 대해서는 0으로 채웠다.

위에서 만든 user-movie 테이블을 transpose하여 movie-user 테이블로 만든다.

TruncatedSVD를 scikit-learn 으로 부터 불러온다.
여기서 TruncatedSVD란,

일반적인 SVD와 달리 상위 몇개의 singular value만 골라내어 사용한다.
(https://darkpgmr.tistory.com/106 에서 truncated SVD를 사용하여 압축한 이미지를 볼 수 있다.)
물론 t를 A의 rank로 설정하면 원래의 SVD이다.
위에서는 t값(n_components)을 12로 하였다.

numpy의 corrcoef를 이용하여 피어슨 상관계수 행렬을 구해주면 9719X9719의 사이즈이다.
(행을 기준으로 계산하기 때문)

user-movie 테이블의 열은 movie title인데 이것을 리스트로 만들고
가디언즈 오브 갤럭시 영화의 인덱스를 찾아주면 3667인것을 확인할 수 있다.
이제 이 가디언즈 오브 갤럭시와 유사한 영화 50개를 찾아보자.
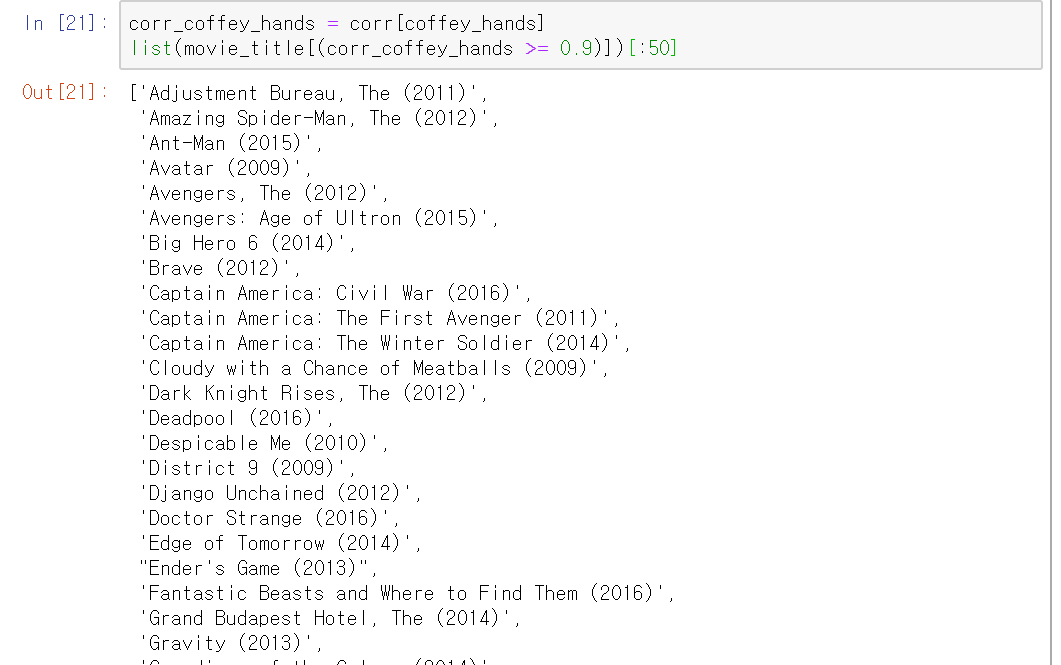
가디언즈 오브 갤럭시와 상관계수값이 0.9이상인 영화 50개를 알려준다.
sorting된 것이 아니라 그냥 원래 저장된 순서대로 알려준다.
여기까지 SVD를 이용한 Collaborative Filtering 추천이였다.
모든 코드 참고 : https://lsjsj92.tistory.com/570
파이썬 Matrix Factorization 영화 추천 시스템(movie recommender system) 구현해보기 - 2
포스팅 개요 해당 글에 대한 코드는 아래 github 링크에 전부 올려두었습니다. https://github.com/lsjsj92/recommender_system_with_Python lsjsj92/recommender_system_with_Python recommender system with Pyt..
lsjsj92.tistory.com
'개발 > Recommender System' 카테고리의 다른 글
| 추천시스템 Collaborative Filtering(CF) Python 기반 [4] (0) | 2020.05.08 |
|---|---|
| 추천시스템 Collaborative Filtering(CF) Python 기반 [3] (0) | 2020.05.08 |
| 추천시스템 Collaborative Filtering(CF) Python 기반 [1] (0) | 2020.04.27 |
| Pandas Library만을 이용하여 간단한 Content Based Filtering 구현하기 (0) | 2020.04.27 |
| Coursera 강의 리뷰 2 - TFIDF and Content-Based Filtering (0) | 2020.04.23 |





댓글