저번 포스팅에서는 가장 단순한 MF인 SVD를 이용하여 구현했었는데,
https://simonezz.tistory.com/25
추천시스템 Collaborative Filtering(CF) Python 기반 [3]
저번 포스팅에서는 SVD를 이용한 CF에 대해 다뤘다. 개인 맞춤형이 아닌 특정영화와 유사한 영화를 평점 행렬 기준으로 추천했었다. 이번 포스팅에서는 개인의 기존 평가를 기반으로 영화를 추천해주는 추천시스템..
simonezz.tistory.com
이번 포스팅에서는 Matrix Factorization을 이용한 CF방식 중 Banila-MF를 이용하여 구현해보고자 한다.

Matrix Factorization은 dimension reduction방법 중 하나로
training matrix R이 주어졌을 때 matrix P와 Q를 찾는 방법이다. 이로인해 아직 평가되지 않은 항목에 관해 예측이 가능하다.

위에서 언급한 바와 같이 training를 위해서는 training matrix R이 있어야 하고 업데이트(minimization)를 통해 P와 Q를 곱한 행렬이 R로 가는 것이 목적이다. 이 업데이트 방법으로는 NNMF, ALS등이 있다.
먼저 User-Item rating matrix를 R이라 하고 이를 P와 Q로 분해하고자 한다. 여기서 P와 Q의 값들이 학습되어야 하는 변수들이다.
그다음 cost에 대해 알아보자.
cost는 실제값과 예측한 값의 차이를 말하는데 간단하게 RMSE(Mean Squared Error의 Root값)를 사용해보자.
이 cost를 minimization하는 것이 목표이다.
minimization으로는 gradient descent를 이용한다.
필요한 수식들을 살펴보면,
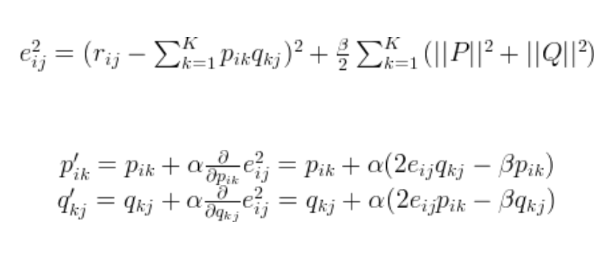
R의 i,j번째 원소인 rij에서 변수 (PQ)ij를 빼고 제곱한 것과 행렬 P와 Q의 놈값을 더한 걸 i,j번째 cost로 정의하고
아래에서는 gradient descent방법으로 P,Q를 각각 update한다. (alpha는 learning rate)
이제 파이썬을 이용하여 구현해보자.
https://yamalab.tistory.com/92?category=747907님의 코드
import numpy as np
class MatrixFactorization():
def __init__(self, R, k, learning_rate, reg_param, epochs, verbose=False):
"""
:param R: rating matrix
:param k: latent parameter
:param learning_rate: alpha on weight update
:param reg_param: beta on weight update
:param epochs: training epochs
:param verbose: print status
"""
self._R = R
self._num_users, self._num_items = R.shape
self._k = k
self._learning_rate = learning_rate
self._reg_param = reg_param
self._epochs = epochs
self._verbose = verbose
def fit(self):
"""
training Matrix Factorization : Update matrix latent weight and bias
참고: self._b에 대한 설명
- global bias: input R에서 평가가 매겨진 rating의 평균값을 global bias로 사용
- 정규화 기능. 최종 rating에 음수가 들어가는 것 대신 latent feature에 음수가 포함되도록 해줌.
:return: training_process
"""
# init latent features
self._P = np.random.normal(size=(self._num_users, self._k))
self._Q = np.random.normal(size=(self._num_items, self._k))
# init biases
self._b_P = np.zeros(self._num_users)
self._b_Q = np.zeros(self._num_items)
self._b = np.mean(self._R[np.where(self._R != 0)])
# train while epochs
self._training_process = []
for epoch in range(self._epochs):
# rating이 존재하는 index를 기준으로 training
for i in range(self._num_users):
for j in range(self._num_items):
if self._R[i, j] > 0:
self.gradient_descent(i, j, self._R[i, j])
cost = self.cost()
self._training_process.append((epoch, cost))
# print status
if self._verbose == True and ((epoch + 1) % 10 == 0):
print("Iteration: %d ; cost = %.4f" % (epoch + 1, cost))
def cost(self):
"""
compute root mean square error
:return: rmse cost
"""
# xi, yi: R[xi, yi]는 nonzero인 value를 의미한다.
# 참고: http://codepractice.tistory.com/90
xi, yi = self._R.nonzero()
predicted = self.get_complete_matrix()
cost = 0
for x, y in zip(xi, yi):
cost += pow(self._R[x, y] - predicted[x, y], 2)
return np.sqrt(cost) / len(xi)
def gradient(self, error, i, j):
"""
gradient of latent feature for GD
:param error: rating - prediction error
:param i: user index
:param j: item index
:return: gradient of latent feature tuple
"""
dp = (error * self._Q[j, :]) - (self._reg_param * self._P[i, :])
dq = (error * self._P[i, :]) - (self._reg_param * self._Q[j, :])
return dp, dq
def gradient_descent(self, i, j, rating):
"""
graident descent function
:param i: user index of matrix
:param j: item index of matrix
:param rating: rating of (i,j)
"""
# get error
prediction = self.get_prediction(i, j)
error = rating - prediction
# update biases
self._b_P[i] += self._learning_rate * (error - self._reg_param * self._b_P[i])
self._b_Q[j] += self._learning_rate * (error - self._reg_param * self._b_Q[j])
# update latent feature
dp, dq = self.gradient(error, i, j)
self._P[i, :] += self._learning_rate * dp
self._Q[j, :] += self._learning_rate * dq
def get_prediction(self, i, j):
"""
get predicted rating: user_i, item_j
:return: prediction of r_ij
"""
return self._b + self._b_P[i] + self._b_Q[j] + self._P[i, :].dot(self._Q[j, :].T)
def get_complete_matrix(self):
"""
computer complete matrix PXQ + P.bias + Q.bias + global bias
- PXQ 행렬에 b_P[:, np.newaxis]를 더하는 것은 각 열마다 bias를 더해주는 것
- b_Q[np.newaxis:, ]를 더하는 것은 각 행마다 bias를 더해주는 것
- b를 더하는 것은 각 element마다 bias를 더해주는 것
- newaxis: 차원을 추가해줌. 1차원인 Latent들로 2차원의 R에 행/열 단위 연산을 해주기위해 차원을 추가하는 것.
:return: complete matrix R^
"""
return self._b + self._b_P[:, np.newaxis] + self._b_Q[np.newaxis:, ] + self._P.dot(self._Q.T)
def print_results(self):
"""
print fit results
"""
print("User Latent P:")
print(self._P)
print("Item Latent Q:")
print(self._Q.T)
print("P x Q:")
print(self._P.dot(self._Q.T))
print("bias:")
print(self._b)
print("User Latent bias:")
print(self._b_P)
print("Item Latent bias:")
print(self._b_Q)
print("Final R matrix:")
print(self.get_complete_matrix())
print("Final RMSE:")
print(self._training_process[self._epochs-1][1])
# run example
if __name__ == "__main__":
# rating matrix - User X Item : (7 X 5)
R = np.array([
[1, 0, 0, 1, 3],
[2, 0, 3, 1, 1],
[1, 2, 0, 5, 0],
[1, 0, 0, 4, 4],
[2, 1, 5, 4, 0],
[5, 1, 5, 4, 0],
[0, 0, 0, 1, 0],
])
# P, Q is (7 X k), (k X 5) matrix
factorizer = MatrixFactorization(R, k=3, learning_rate=0.01, reg_param=0.01, epochs=300, verbose=True)
factorizer.fit()
factorizer.print_results()추후에 이어나갈예정..
'개발 > Recommender System' 카테고리의 다른 글
| 추천시스템 Collaborative Filtering - Model based approach (0) | 2020.05.31 |
|---|---|
| 추천시스템 Recommender System 정리 (0) | 2020.05.26 |
| 추천시스템 Collaborative Filtering(CF) Python 기반 [3] (0) | 2020.05.08 |
| 추천시스템 Collaborative Filtering(CF) Python 기반 [2] (0) | 2020.05.06 |
| 추천시스템 Collaborative Filtering(CF) Python 기반 [1] (0) | 2020.04.27 |





댓글